新型コロナウィルス感染者数の予想値から想定を超えた事態？！

2020.03.31 Selfish Study 0 Comment boff 197 views

昨年末から世界で感染が拡大している新型コロナウィルス。
国内における今後の感染拡大状況について、「指数平滑法」と「残差平方和」を使って統計学的に予想してみました。
使う分析手法は「指数平滑法」と「残差平方和」です。

データ分析はExcelを使います。
指数平滑法は「分析ツール^†1」、残差平方和は「関数（SUMXMY2）」です。
手順としては、指数平滑法で予想値を算出し、どの予想値の精度が高いかを残差平方和で判断します。

データの整理

まず、厚生労働省の最新のデータ（「新型コロナウイルス感染症に関する報道発表資料（発生状況、国内の患者発生、海外の状況、その他）」厚生労働省）である2020年3月30日からさかのぼって、次のように1週間ごと10週に区切りました。

1週（1/21～1/27）
2週（1/28～2/3）
3週（2/4～2/10）
4週（2/11～2/17）
5週（2/18～2/24）
6週（2/25～3/2）
7週（3/3～3/9）
8週（3/10～3/16）
9週（3/17～3/23）
10週（3/24～3/30）

そして予想するのは「11週（3/31～4/6）の国内感染者数」ということにします。

Excelに入力し整理した実数値データは次のような感じです。

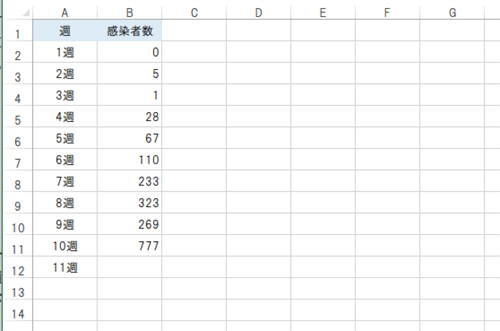
指数平滑法で予想値を算出

指数平滑法は、実績値から予想値がどれだけ外れているかを計算し、それに係数（減衰率）を乗じて得た修正値を、直前の予想値に加減して新たな予想値を導き出す手法です。
係数は1未満（0<係数<1）を設定しますが、1に近いほど直前のデータの影響が大きく、0に近いほど過去の経過を重視することになります。

Excelで指数平滑法は、データ→データ分析→分析ツール「指数平滑」を選びます。
ちなみに、Excelで指数平滑法を使うには、4つ以上のデータが必要です。

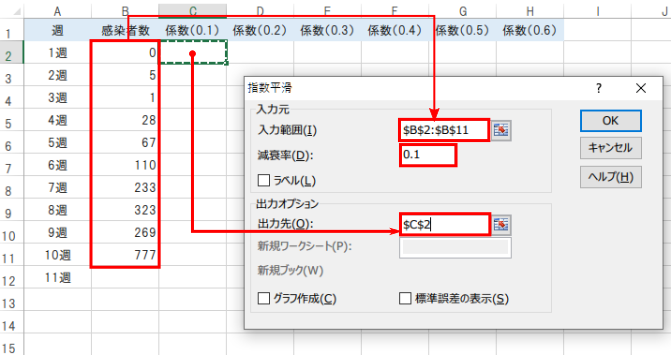
入力範囲は準備したデータ（感染者数）範囲、減衰率は係数（1未満の小数）、出力先は各係数の「1週」のセルを選択します。
係数（減衰率）については、0.1～0.6までの予想値を算出し、残差平方和でどの予想値の精度が高いかを判断することにします。

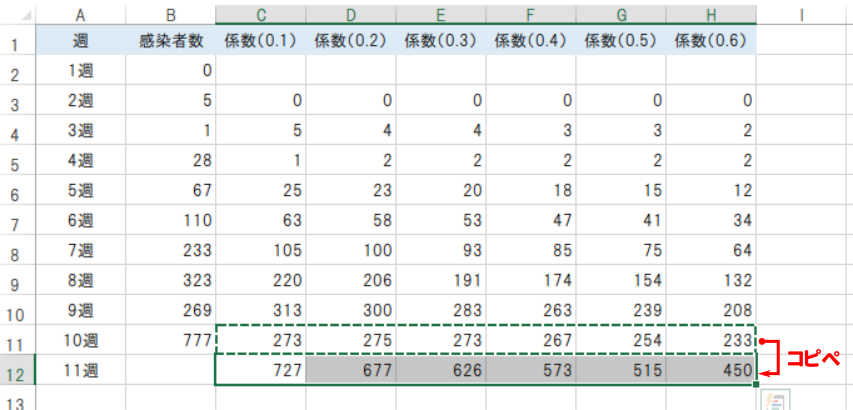
指数平滑法の係数0.1～0.6で算出した最後のデータ行（10週）をコピーして、そのすぐ下の行にペーストすると、各係数の11週における感染者数の予想値が表示されます。

残差平方和で予想値の精度を判断

指数平滑法の各係数で予想値が算出されましたが、どの予想値を採用するか判断する必要があります。
そこで残差平方和（SUMXMY2）を利用します。

残差平方和とは、実数値と予想値の差（距離）を2乗しその合計値を返す関数です。
つまり、実数値と予想値の差を面積として捉え、その面積が小さければ誤差が小さいと判断することができます。

残差平方和は、数式→関数の挿入→関数の検索で「残差平方和」か「SUMXMY2」で検索開始→「SUMXMY2」を選びます。

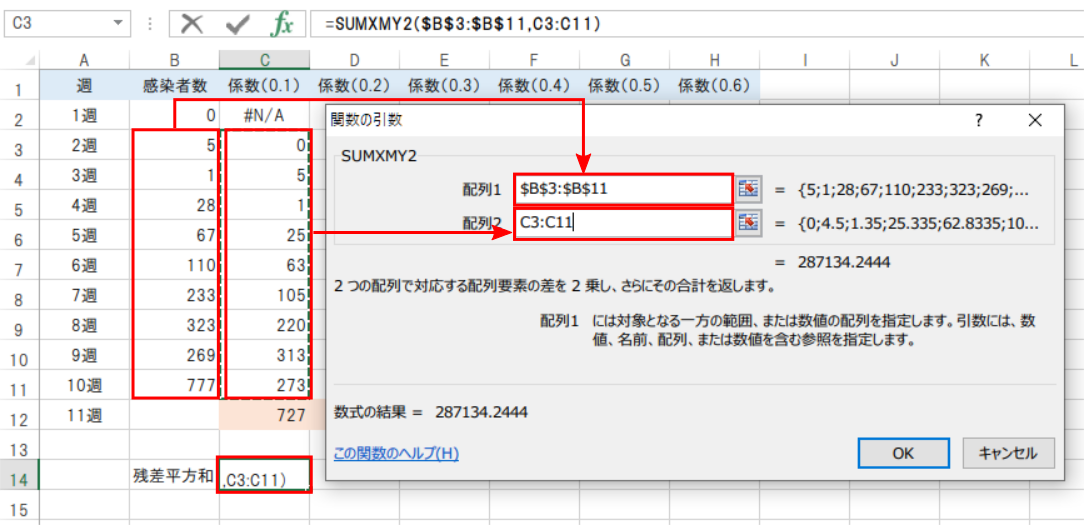
関数の出力先を「C14」にします。
SUMXMY2を選択し、配列1は準備した2週～10週のデータ（感染者数）、配列2は指数平滑法で算出した予想値も同じく2週～10週を範囲選択します。
この際、配列1は絶対指定（$B$3:$B$11）しておきましょう。

そして、C14セルをコピーし、となりの各係数のセル（D14～H14）にペーストすると計算結果が表示されます。

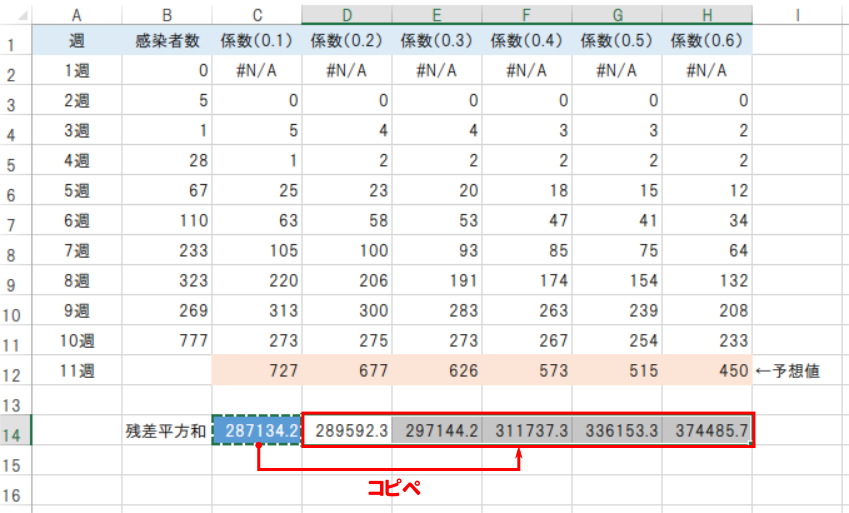
各係数の残差平方和を見ると、係数（0.1）の値が最も小さいことから、11週の予想値は係数0.1で求めた「727」が最も精度が高いと判断されます。

感染者の予想値と想定を超える結論

指数平滑法を用いて11週（3月31日～4月6日）の感染者数を予想すると、727人と導き出すことができました。

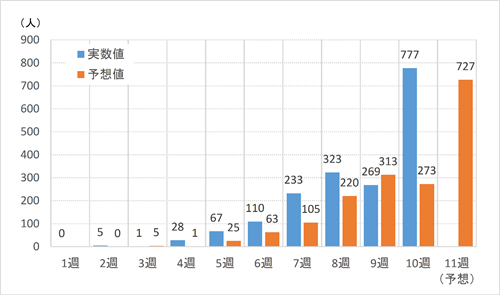
ここで注目すべき点は、10週の値です。
実数値は777人、予想値は273人であり、データの乖離が明らかに大きくなっています。
つまり、統計的予想値をはるかに超えて、実際に感染者が増えているということを示しています。

安倍晋三内閣総理大臣は3月14日の記者会見で「現時点では爆発的な感染拡大には進んでおらず、一定程度、持ちこたえている」、3月28日には「ぎりぎり持ちこたえている状況」と発言しています。
確かに3月14日時点（8週）から9週までは感染者の実数値は大幅には増えおらず、予想値も近い値を示しています。
しかしながら、新型コロナウィルスは約2週間の潜伏期間があるとされており、3月14日の会見から2週間後である10週（3月24日～3月30日）には感染者数が一気に急増しました。
統計データから考えると、残念ながら3月14日の会見以降の政府による新型コロナウィルス対策は、瀬戸際を防げなかったのではないかと評価できそうです。
また、10週の予想をはるかに超える感染者の増加からしても、指数平滑法による11週の予想値は妥当性を欠いており、もしかしたら予想値を倍増するのではないかと危惧します。

引き続き11週（3月31日～4月6日）の感染者数の実数値がどうなるかを見れば、日本国内における感染拡大防止策は効果を発揮しているのか？ひとつの判断材料になるのではないでしょうか。