Marble-Lab

実際の調査データを使ってカイ二乗検定をやってみます。

カイ二乗検定は、グループ間における比率の偏り（関連）を検証する場合に用いられ、独立性の検定と適合度の検定があります。

■独立性の検定
グループと回答比率との独立性（関係性）の有無を検証。

例えば、性別や年齢別に選択肢の比率に偏り（関連）があるかどうかを判断する場合。

 

■適合度の検定
母集団の比率と調査結果のそれとの偏りの有無を検証。

いずれも、有意水準に比べ有意確率が、低ければ何らかの偏り（関連）があると判断し、高ければ偏り（関連）はないと判断します。

検定そのものの考え方は「『検定』について考える」を参照してください。

計算についてはExcelを使用しました。

独立性の検定：2×2分割表

グループもカテゴリー数もいずれも2つずつの場合、「2×2分割表」の算出方法を用いてカイ二乗検定を行うことができます。

例えば、次のような調査結果が得られました。
性別でみると、男性に比べて女性で「正規雇用」の割合が低く「非正規雇用」の割合が高い傾向があります。

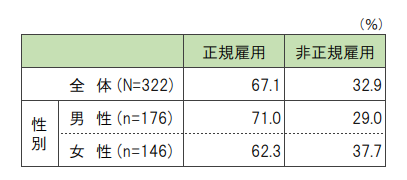
では、本当に性別間で比率に何からの関連があると言えるのか、カイ二乗検定をしてみましょう。

対立仮説は「性別間に比率の偏りがある」、帰無仮説は「性別間に比率の偏りはない」、有意水準は5％（0.05）とします。
カイ二乗検定は、比率ではなく実数を使って計算します。

下表は上表の比率を実数にしたものです。

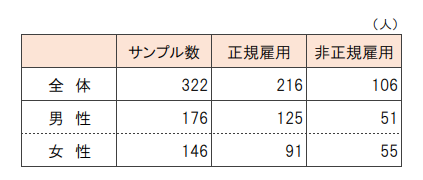
2×2分割表のカイ二乗値を求める数式と、数式に代入する実数値の対応は次のとおりです。

数式に当てはめて計算した結果は次のとおりです。

有意確率の計算

算出したカイ二乗値と自由度からExcel関数の「CHISQ.DIST.RT（カイ二乗値, 自由度）」を使って有意確率（p値）を求めます。
自由度は「（グループ数-1）×（カテゴリー数-1）」で求めるので、今回のケースでは（2-1）×（2-1）＝1です。

Excelで「=CHISQ.DIST.RT(2.731, 1)」と入力すると、「0.10」（小数第三位を四捨五入）という結果が返ってきました。

有意確率（p値）は0.10であり有意水準0.05を上回っているため、帰無仮説は棄却されません。
つまり、「性別間において偏りは認められない」ということが明らかになりました。

レポーティングはどう書く？

最後に、今回の検定結果を調査報告書や論文に書く場合の記述例を参考までに記しておきます。

性別ごとの雇用条件（正規・非正規）について有意水準5％でカイ二乗検定を行ったところ、関連は認められなかった（χ2（1, N = 322) = 2.73, p = .10）。したがって、性別で雇用条件に差異があるとは言えない。

ちなみに、カッコの中の「1」は自由度、「N=」はサンプル数^†1です。

マンガでわかる統計学 素朴な疑問からゆる~く解説 (サイエンス・アイ新書)

posted with amazlet at 19.02.15

大上 丈彦
SBクリエイティブ
売り上げランキング: 560

Amazon.co.jpで詳細を見る